漸近線とは「しだいに近づいていく直線」のことです。 「しだいに近づいていく」をもう少しきちんと言うと「十分遠くで距離が限りなく $0$ に近づいていく」です。この説明でだけでは漸近線の意味が分かりにくいので、3つの具体的な漸近線のパターンを数学3極限・漸近線の求め方 数学の漸近線の求め方で分からないところがあります。 f(x)=(x^21)^(3/2)(x^3) の漸近線を求める問題で 分子分母にf(x)(axb)をかけて求めればいいらしいのですが さっぱり分かりません。数列の極限の求め方(基本) 数列の一般項が不定形の場合は、式変形して、\(\frac{1}{n}\)の式になるように表し、\(\frac{1}{n}\)の部分を0に置き換えると極限が求められます。 不定形のままでは極限は求められません。 よくでてくる不定形の形を下記に示します。

標準 微分と関数のグラフと漸近線 なかけんの数学ノート
漸近線 求め方 極限
漸近線 求め方 極限-//始点のx座標 const h = range;数学3極限・漸近線の求め方 数学の漸近線の求め方で分からないところがあります。 f(x)=(x^21)^(3/2)(x^3) の漸近線を求める問題で 分子分母にf(x)(axb)をかけて求めればいいらしいのですが さっぱり分かりません。



漸近線の求めかた Y X 1 1 X 1 のグラフを描く問題なんですが 数学 教えて Goo
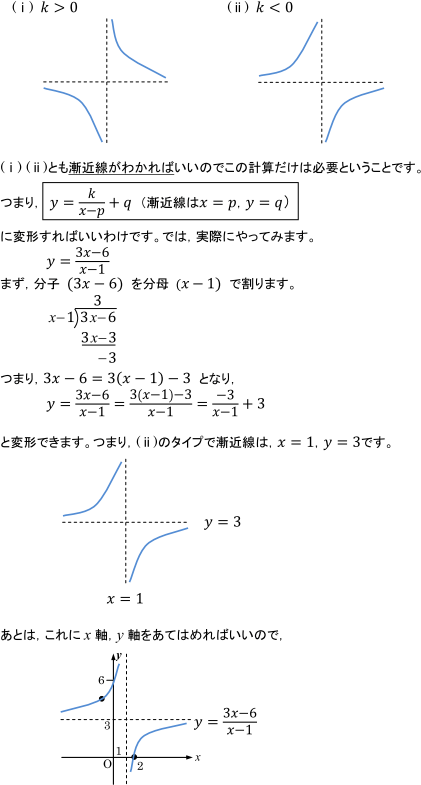
そこで, x→∞, x→−∞ のときの極限を考えると, となり, x→∞, x→−∞ のとき, yは0に限りなく近づく, すなわち, x軸が漸近線であることがわかるので, 図2のようなグラフになることがわかります。 これより, yの増減表を次のようにするとなんで漸近線を持つ直角双曲線がこのような形になるんですか?? この形は分数関数の形じゃないですか! の漸近線の求め方が分かりません。 x=1になるのはわかるのですが、なぜy=1になるのでしょうか? また極限を調べるときはx→∞を調べないとこれを利用して右側微分と左側微分を求め,その値が異なる点を漸近線として判定します。 const Range = 18;
見て頂いてありがとうございます. 見てもらうために作成しておりますので,どんどん見てください.★の数は優先度です.★→★★→★★★ の順に取り組みましょう.3211←→ ポイント集をまとめて見たい場合 点線より下側のここでは、関数のグラフをかくときに必要となる、漸近線について見ていきます。 定義域の境目や端っこについて 例題 次の関数の増減、極値、凹凸、漸近線を調べて、グラフをかきなさい。 y=x dfrac{1}{x}数学3極限・漸近線の求め方 数学の漸近線の求め方で分からないところがあります。 f(x)=(x^21)^(3/2)(x^3) の漸近線を求める問題で 分子分母にf(x)(axb)をかけて求めればいいらしいのですが さっぱり分かりません。
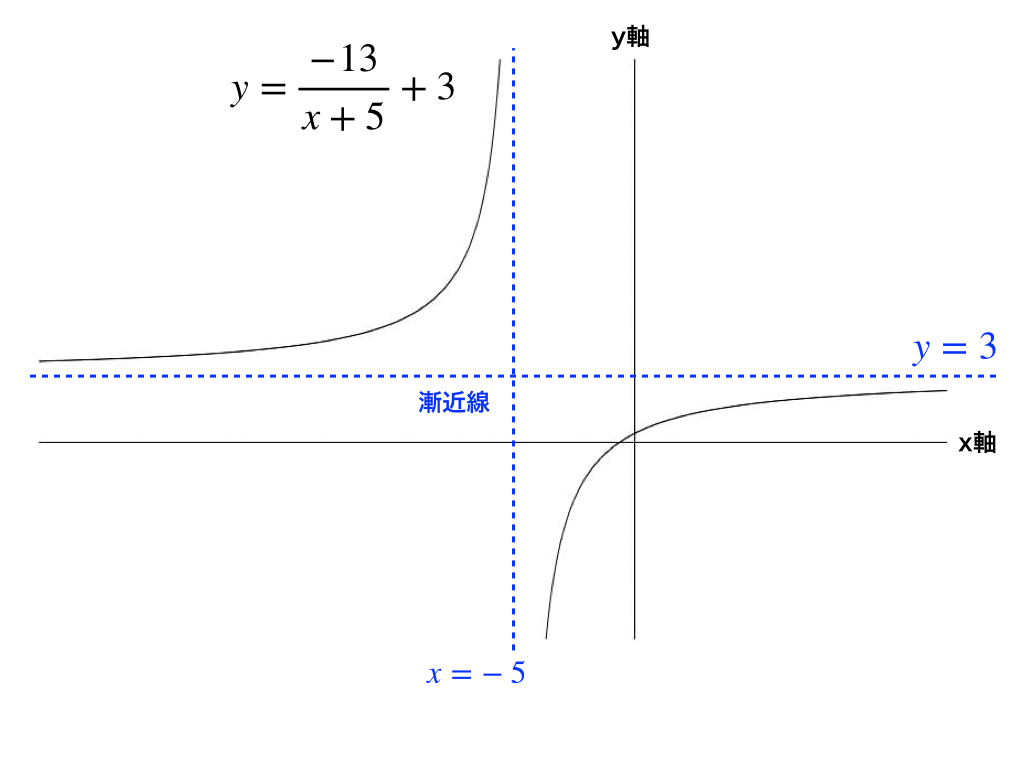
X が負の無限大に接近する場合の極限もまた 3 になります。この結果は、 y = 3 のラインが、 f の水平方向の漸近線であることを意味しています。 f の垂直方向の漸近線を求めるには、分母を 0 に等しくなるように設定して、それを解きます。Let x = Range / 2;漸近線を持つ代表的な関数 漸近線はない場合もありますし、複数ある場合もあります。 ですが漸近線を必ず持つとわかっている関数がいくつかあるので、最低限これらの関数は押さえておきましょう。 指数関数 \(y=2^x,y=2^{x}\)はグラフのようになりますが、\(x\)軸に着目すると漸近線である
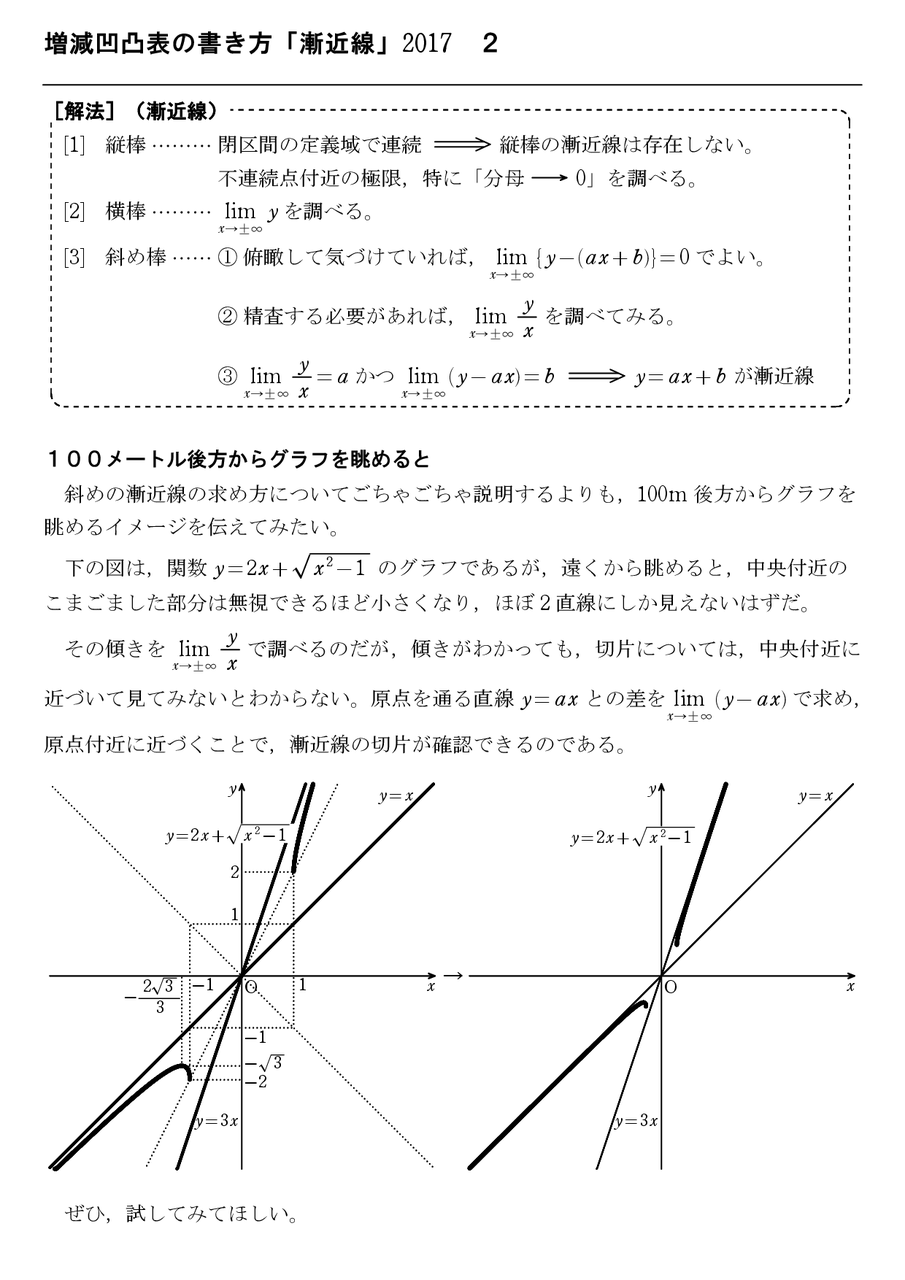


増減凹凸表の書き方 漸近線 17 2 怜悧玲瓏 高校数学を天空から俯瞰する
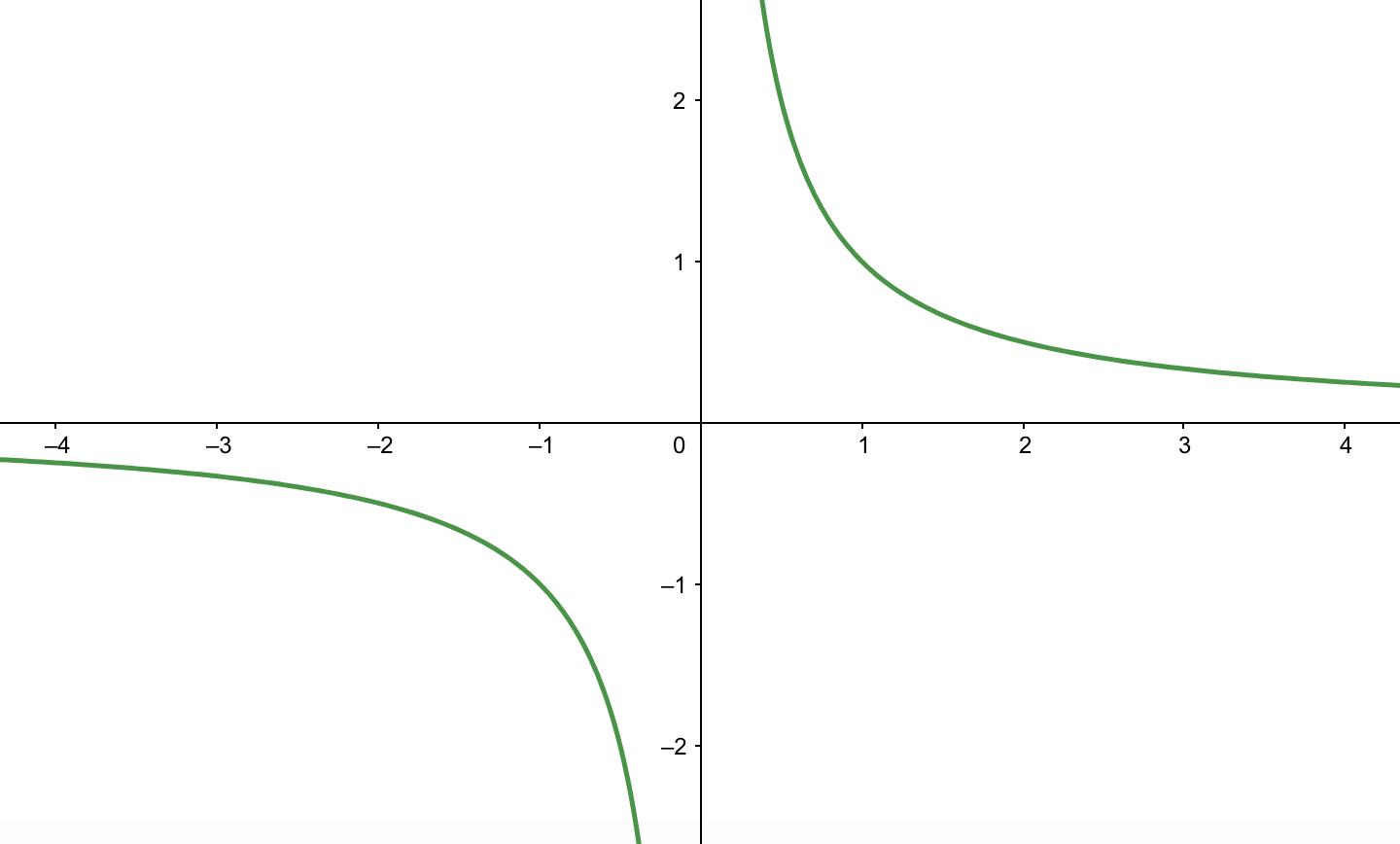


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
ここでは極限のイメージから漸近線を導いてみます。 数Ⅱ軌跡と領域領域はタテ方向で考える 線形計画法における最大・最小の求め方 1909 0901 1/1x^2 型の積分 tan に置きかえる漸近線である。 漸近線の求め方 y=f(x) の漸近線がy ax b とすると,x が+∞ある いは-∞のとき,y の値はほぼ同じと考えられるので, f(x)≒ax+b ・・・① とおける。両辺をx で割って,lim計算すると, lim( ) ( ) lim x b a x f x x x よって, x f x a x ( ) lim曲線に対する漸近線の求め方 f (x) = 3x2−5x x−2 f ( x) = 3 x 2 − 5 x x − 2 の漸近線を求めよ。 画像を見ればわかりますが、答えは、 x = 2, y = 3x 1 x = 2, y = 3 x 1 このような問題を解くために、 曲線 y = f (x) y = f ( x) の漸近線が直線 y = ax b y = a x b であるとき


漸近線の方程式


漸近線の方程式
ここではあくまでも漸近展開を使っても極限が求められるということを紹介しました ただし, どこまでの漸近展開が必要かはわからないところがこれの喰えないところでもあります exercise4 以下の関数の極限を漸近展開を用いて求めましょう (1)よって漸近線は x=-2 と y=x-4 漸近線の求め方 y軸に平行な漸近線x→a+oのとき=±∞ のとき x=aは漸近線 y軸に平行でない漸近線 lim(x→±∞)f(x)-(ax+b)=0ならいただいた nb を見て、漸近線の求め方の別解?も「2次曲線について4.」としてブログにあげさせてもらいました。ありがとうございます。 整数解の方は、Wolfram alpha に解かせたところ、無限個あるようですね。



Y Ax B 2x 1 1 のグラフが点 1 0 Okwave



漸近線の求め方 高校数学 微分法の応用 15 Youtube
見て頂いてありがとうございます. 見てもらうために作成しておりますので,どんどん見てください.★の数は優先度です.★→★★→★★★ の順に取り組みましょう.3332 30←→ ポイント集をまとめて見たい場合 点線漸近線 漸近線 定義域 値域 例題1)関数 \ のグラフをかけ。また,その定義域と値域を求めよ。 s よって \ 分母 とすると に変えると とすると \ に変えると \ ゆえに,グラフは右の図の直角双曲線で,漸近線は 2 直線 ,\ である。// x軸両端の幅 const range = Range / 400;
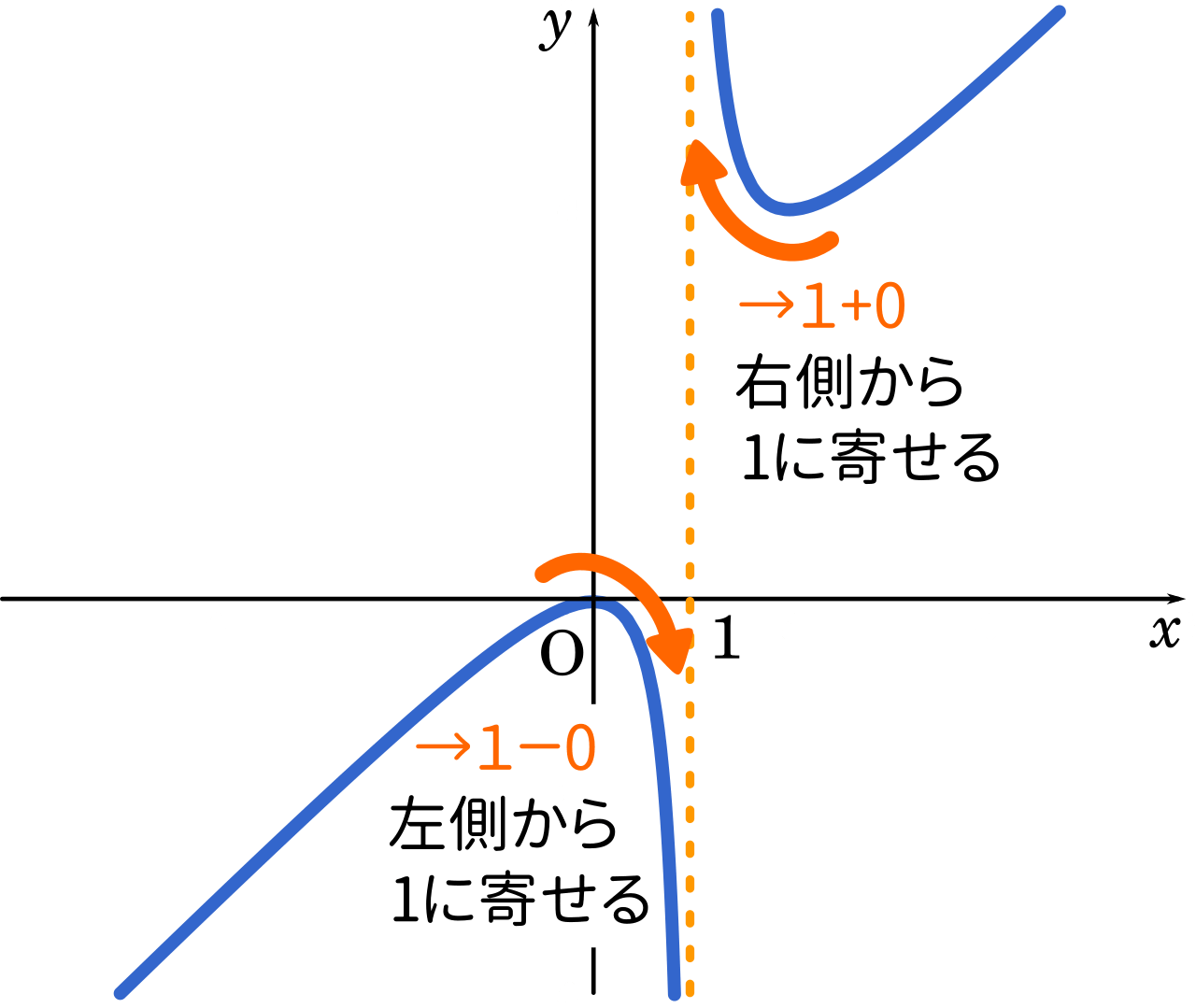


数 微分の応用 ざっくりイメージから漸近線を導く Mm参考書



漸近線公式 雙曲線 漸近線の求め方 導出方法あり 5分でわかる Krgez
ここではあくまでも漸近展開を使っても極限が求められるということを紹介しました ただし, どこまでの漸近展開が必要かはわからないところがこれの喰えないところでもあります exercise4 以下の関数の極限を漸近展開を用いて求めましょう (1)ここでは、関数のグラフをかくときに必要となる、漸近線について見ていきます。 定義域の境目や端っこについて 例題 次の関数の増減、極値、凹凸、漸近線を調べて、グラフをかきなさい。 y=x dfrac{1}{x}そこで,(1)で求めた a を使って, y−ax の極限を求めて,極限値があればこれを b とおきます.(極限値が有限確定でなければこの形の漸近線はないということです.)


y x 2 xの概形をかけという問題なんですが 双曲線以外の図形の漸近線 Yahoo 知恵袋
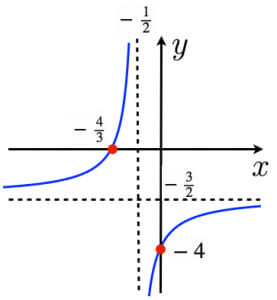


一次分数関数のグラフと漸近線 高校数学の美しい物語
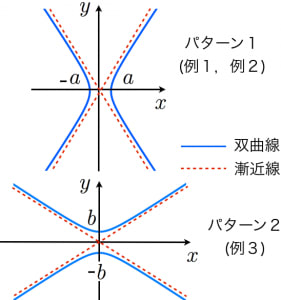
こんにちは、ウチダショウマです。 今日は、数学Ⅱで初めて登場するが詳しくは数学Ⅲで習う 「漸近線」 について、求め方、意味、定義について解説していきます! 主な具体例(分数関数や双曲線)も挙げながら詳しく見ていきましょう♪ 漸近線とは まずは聞き慣れない言葉だと思いますので双曲線の漸近線の簡単な求め方と証明 分野 二次曲線 レベル ★ 入試対策 双曲線の漸近線: パターン1.双曲線 x 2 a 2 − y 2 b 2 = 1 の漸近線は y = ± b a x また, パターン2.双曲線 x 2 a 2 − y 2 b 2 = − 1 の漸近線も y = ± b a x ただし,この記事を通して a, bが現在地です. ※この頁では漸近線の方程式の求め方を解説します. 有限の値 a に対して, x→a のとき y→∞ または y→−∞ になるとき, x=a が漸近線になります. 関数が定義されず, x→1 のとき y→±∞ となります.このとき, x=1 が漸近線になり



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学


基礎数学 3回目
漸近線の方程式 解説 高校の微分積分で漸近線の問題が登場するのは,微分法の応用として,「増減,極値,凹凸,変曲点,漸近線の方程式を求めてグラフの概形を書け」という場面です。 したがって,漸近線の方程式を単独で問うことはまれです。漸近線である。 漸近線の求め方 y=f(x) の漸近線がy ax b とすると,x が+∞ある いは-∞のとき,y の値はほぼ同じと考えられるので, f(x)≒ax+b ・・・① とおける。両辺をx で割って,lim計算すると, lim( ) ( ) lim x b a x f x x x よって, x f x a x ( ) limここでは極限のイメージから漸近線を導いてみます。 数Ⅱ軌跡と領域領域はタテ方向で考える 線形計画法における最大・最小の求め方 1909 0901 1/1x^2 型の積分 tan に置きかえる



漸近線 Wikiwand
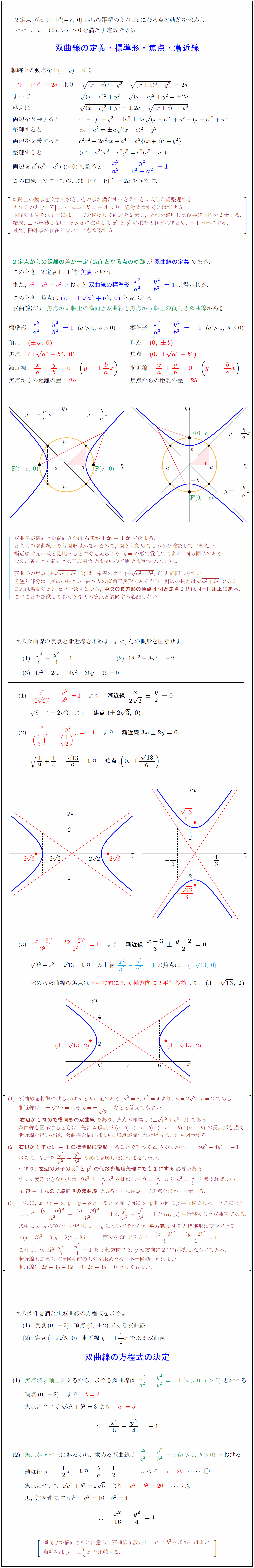


高校数学 双曲線の定義 標準形 焦点 漸近線 双曲線の方程式の決定 受験の月



漸近線の方程式がy 2x 5 Y 2x 3で 点 1 1 を通る双曲線の方程式を その他 教育 科学 学問 教えて Goo
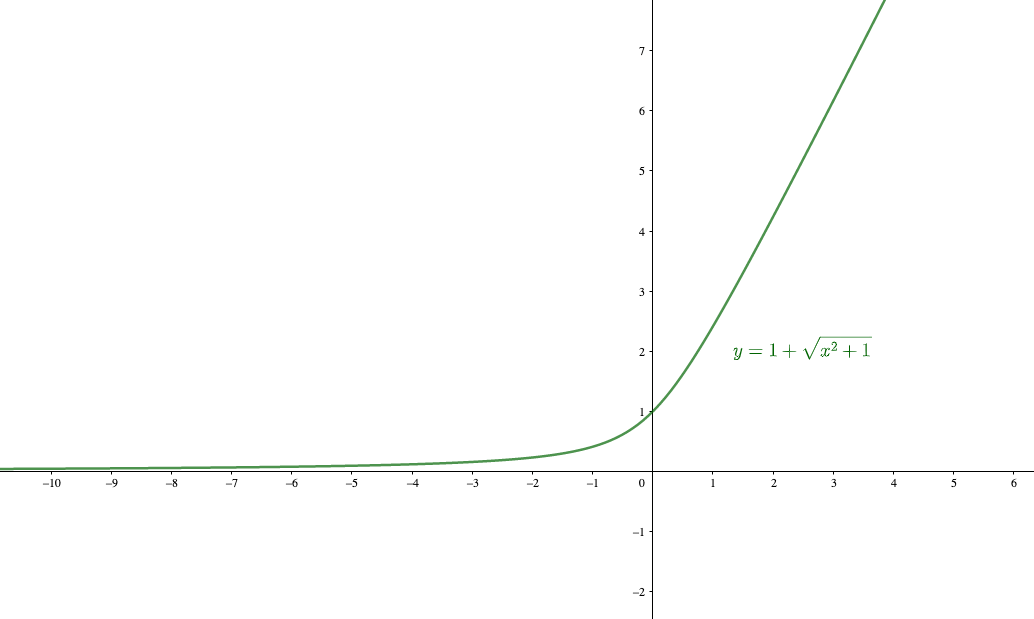


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



漸近線 Wikipedia
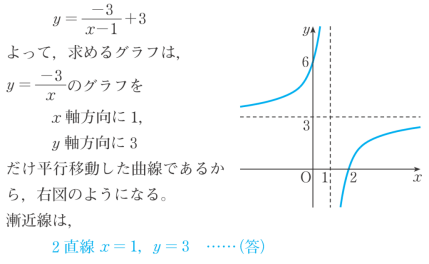


関数と極限 分数関数のグラフのかき方 数学 定期テスト対策サイト



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学



漸近線の求めかた Y X 1 1 X 1 のグラフを描く問題なんですが 数学 教えて Goo



数学 微分法 怜悧玲瓏 高校数学を天空から俯瞰する


右極限と左極限の求め方が分かりません 写真の場合 X 1 1 X Yahoo 知恵袋
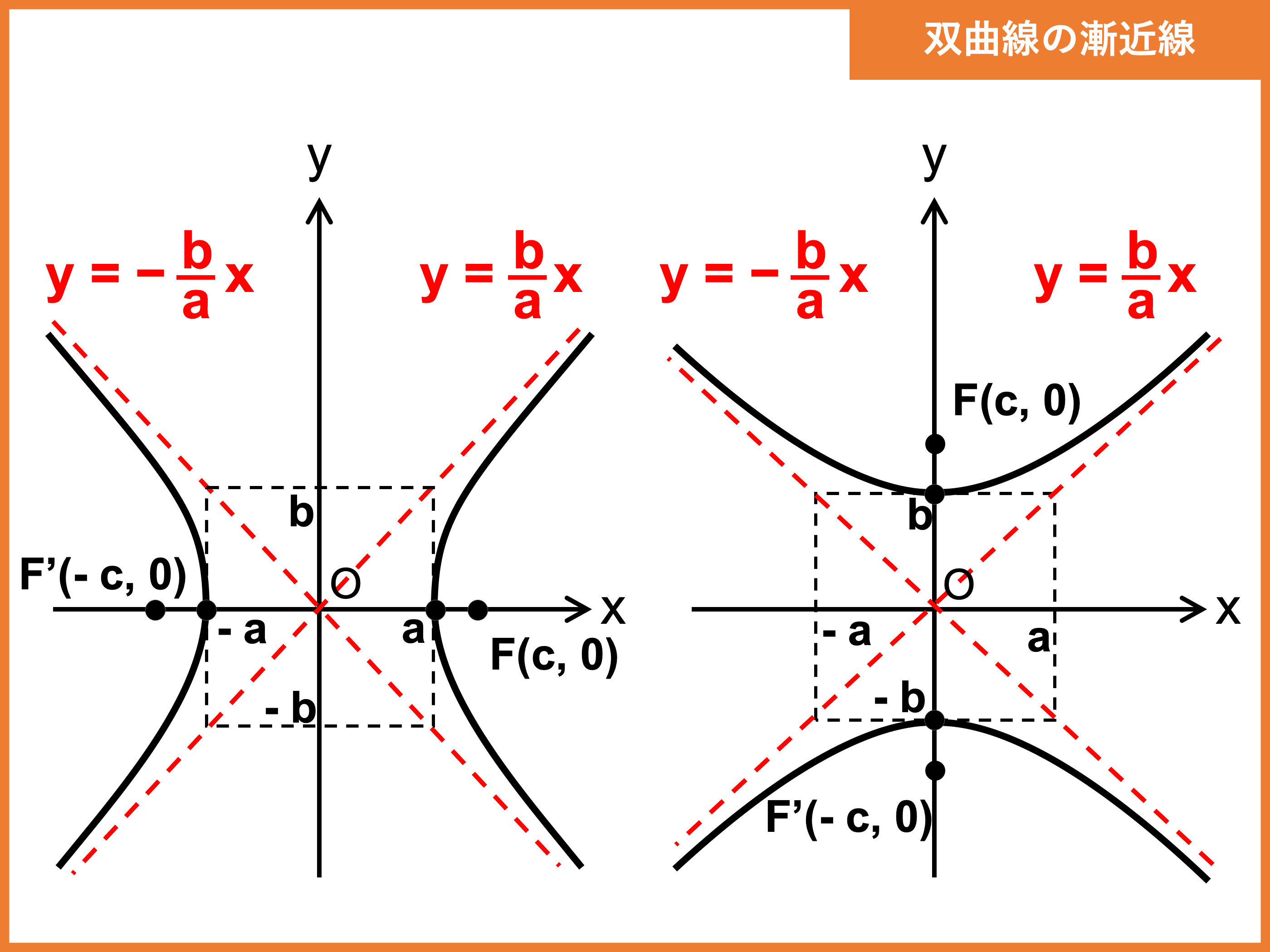


双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典


漸近展開に関するメモ



数3 関数の極限 グラフ 漸近線 高校数学に関する質問 勉強質問サイト
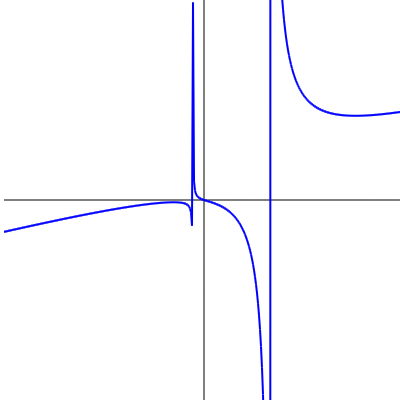


Javascript Y軸に平行な漸近線を描く Mm参考書
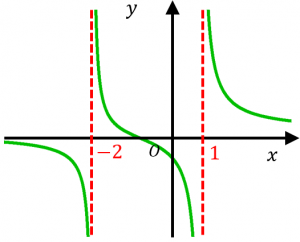


漸近線の求め方3パターン 具体例で学ぶ数学



曲線を無限に遠ざけた時に漸近線に近づいていくという事 高校数学に関する質問 勉強質問サイト



標準 微分と関数のグラフと漸近線 なかけんの数学ノート



高校数学 双曲線のグラフ 1 映像授業のtry It トライイット



Y Tan8のグラフの書き方 三角関数のグラフ 数学ii By ふぇるまー マナペディア
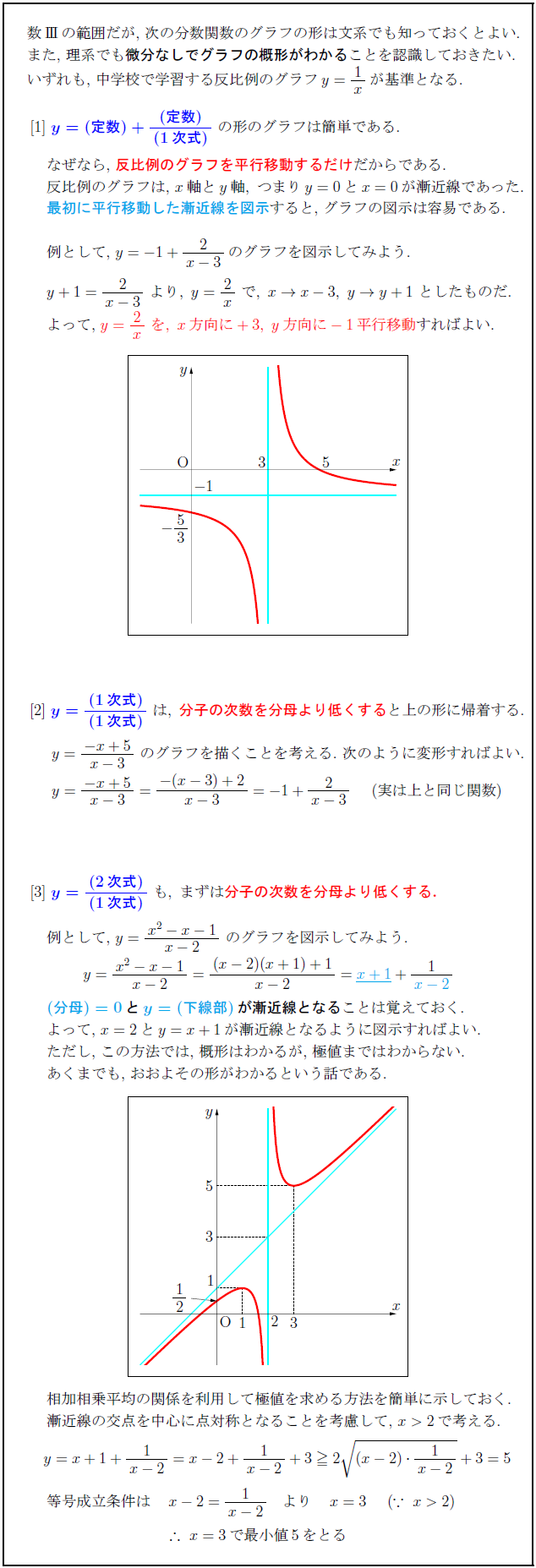


高校数学 文系も知っておくべき基本的な分数関数 数 のグラフ 受験の月



定義域に関する質問 勉強質問サイト
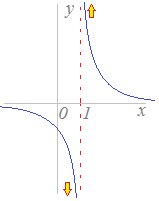


漸近線の方程式


入試問題研究 関西大学19年度



数学 Instagram Posts Gramho Com



高校数学公式集 数学3 C プロシードネットショップ


関数と極限 分数関数のグラフのかき方 数学 定期テスト対策サイト



最大値 最小値 変曲点 Matlab Simulink Example Mathworks 日本


基礎数学 3回目



のx軸に平行な漸近線でlim X F X になった 高校数学に関する質問 勉強質問サイト



数 微分法 漸近線 Y Ax B タイプ オンライン無料塾 ターンナップ Youtube



双曲線とは 例題と要点まとめでマスターしよう 高校生向け受験応援メディア 受験のミカタ



分数関数のグラフの書き方 定義域 漸近線 数学の偏差値を上げて合格を目指す


漸近線 Wikiwand


誤答から学ぼうシリーズ 関数の極限と漸近線 ほのぼの数学頑張ろう



漸近線公式 雙曲線 漸近線の求め方 導出方法あり 5分でわかる Krgez



数学3編 完全攻略 高校数学の公式全部まとめてみたwww Cupuasu クプアス



漸近線 Wikiwand



高校数学 双曲線のグラフ 1 映像授業のtry It トライイット


分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法



漸近線の描き方 一目瞭然早見チャート 高校生 数学のノート Clear



基本 双曲線と漸近線 なかけんの数学ノート
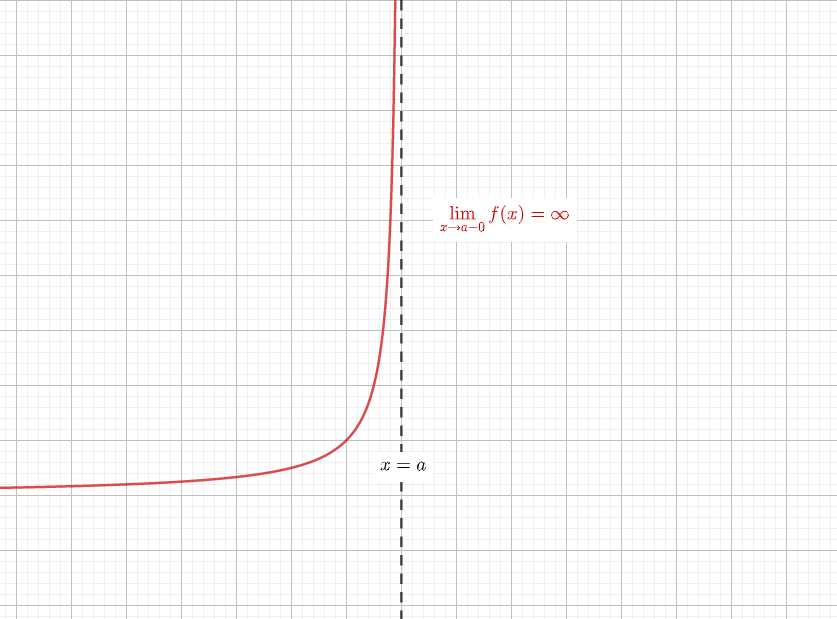


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



高校数学 グラフのかき方 2 問題編 映像授業のtry It トライイット



漸近線の求め方 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc



数学d 1学期 Flashcards Quizlet



漸近線 Wikipedia


双曲線の漸近線の簡単な求め方と証明 高校数学の美しい物語



数学 第10講義 の最初の問題です フォーラム N予備校
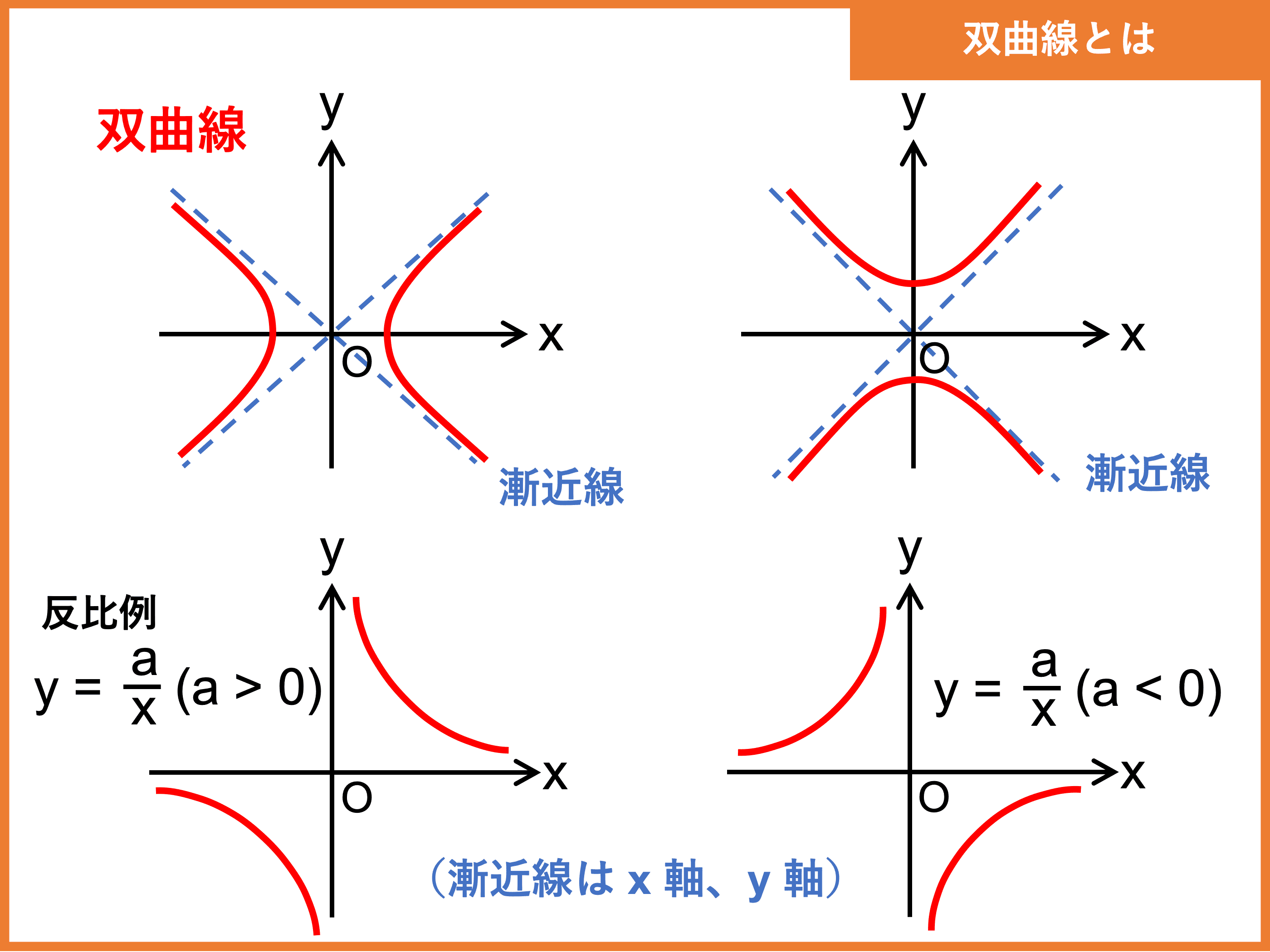


双曲線とは 関数のグラフや式 漸近線や焦点 媒介変数表示など 受験辞典



双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ



漸近線の求め方が分かりません 3 です Clear
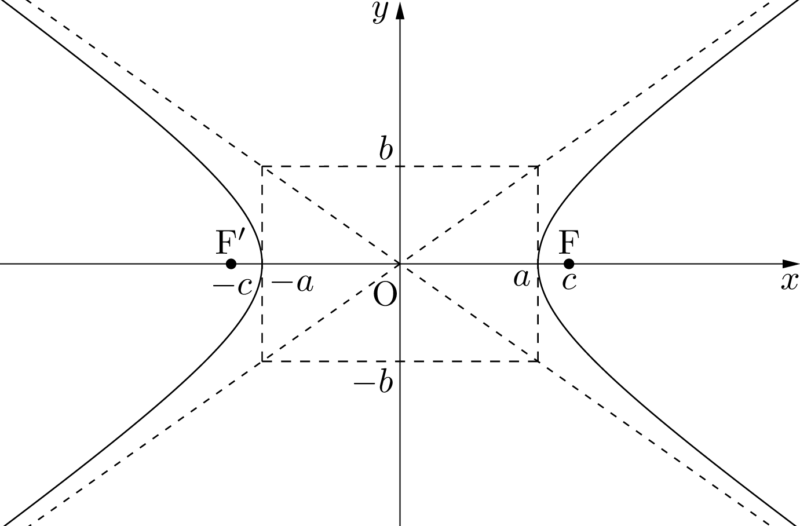


双曲線 焦点 媒介変数表示 極方程式 接線 群馬大 大学入試数学の考え方と解法



分数関数の平行移動 数学iii By Okボーイ マナペディア



漸近線 漸近線の求め方3パターン Edoule



タカタ先生のガチ授業 数 関数と極限 分数関数の漸近線の求め方 裏技 勉強 Youtube スタディチューブ



双曲線の知識まとめ 焦点 漸近線 方程式 媒介変数表示 接線公式 理系ラボ



関数の極限の求め方 その5 積分を含んだ関数と区分求積法 数学の偏差値を上げて合格を目指す



752 これは古典的な双曲線論における 新しい知見です 原点が双曲線上の点と見なされ 漸近線が接戦と見なされることを 述べている 知見 除算



高校数学 漸近線の求め方 前編 増減表で自動化 タテ ヨコ 予想法 Youtube


高校数学 分数関数のポイント整理 双曲線と漸近線 偏差値40プログラマー


誤答から学ぼうシリーズ 関数の極限と漸近線 ほのぼの数学頑張ろう



漸近線の求め方が分かりません 3 です Clear


漸近線 Wikipedia



数 関数と極限 この問題 なんでy X 2が漸近線になると分かるんですか 数学 教えて Goo



数学 第10講義 の最初の問題です フォーラム N予備校
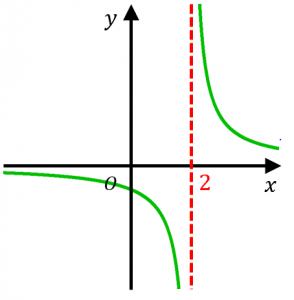


漸近線の求め方3パターン 具体例で学ぶ数学


数3の微分の漸近線を求める時の極限の問題です 高3なの Yahoo 知恵袋
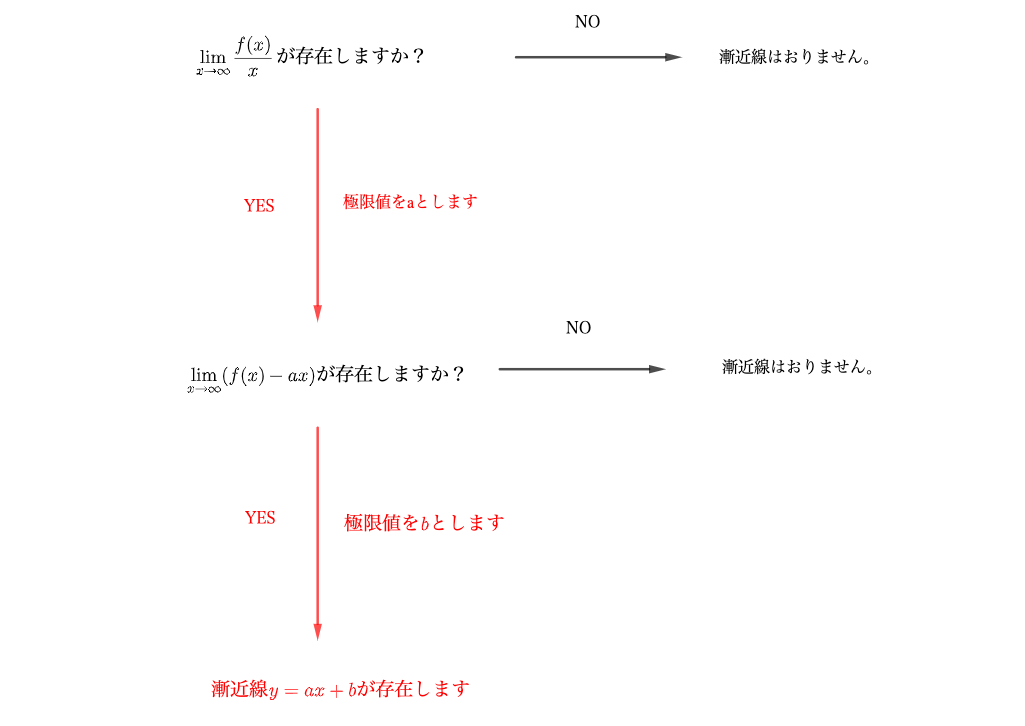


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック
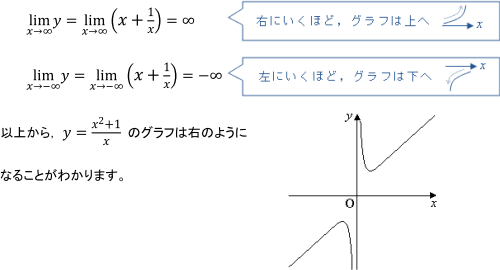


複雑な関数のグラフのかき方 数学 苦手解決q A 進研ゼミ高校講座



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学
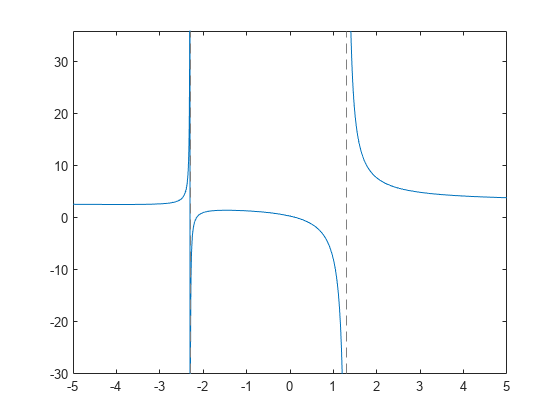


漸近線 臨界点および変曲点を求める Matlab Simulink Mathworks 日本


有理関数のグラフの描き方 医歯薬系数学ラボ



高校数学 陽関数のグラフの図示の基本的な手順とポイントのまとめ 受験の月
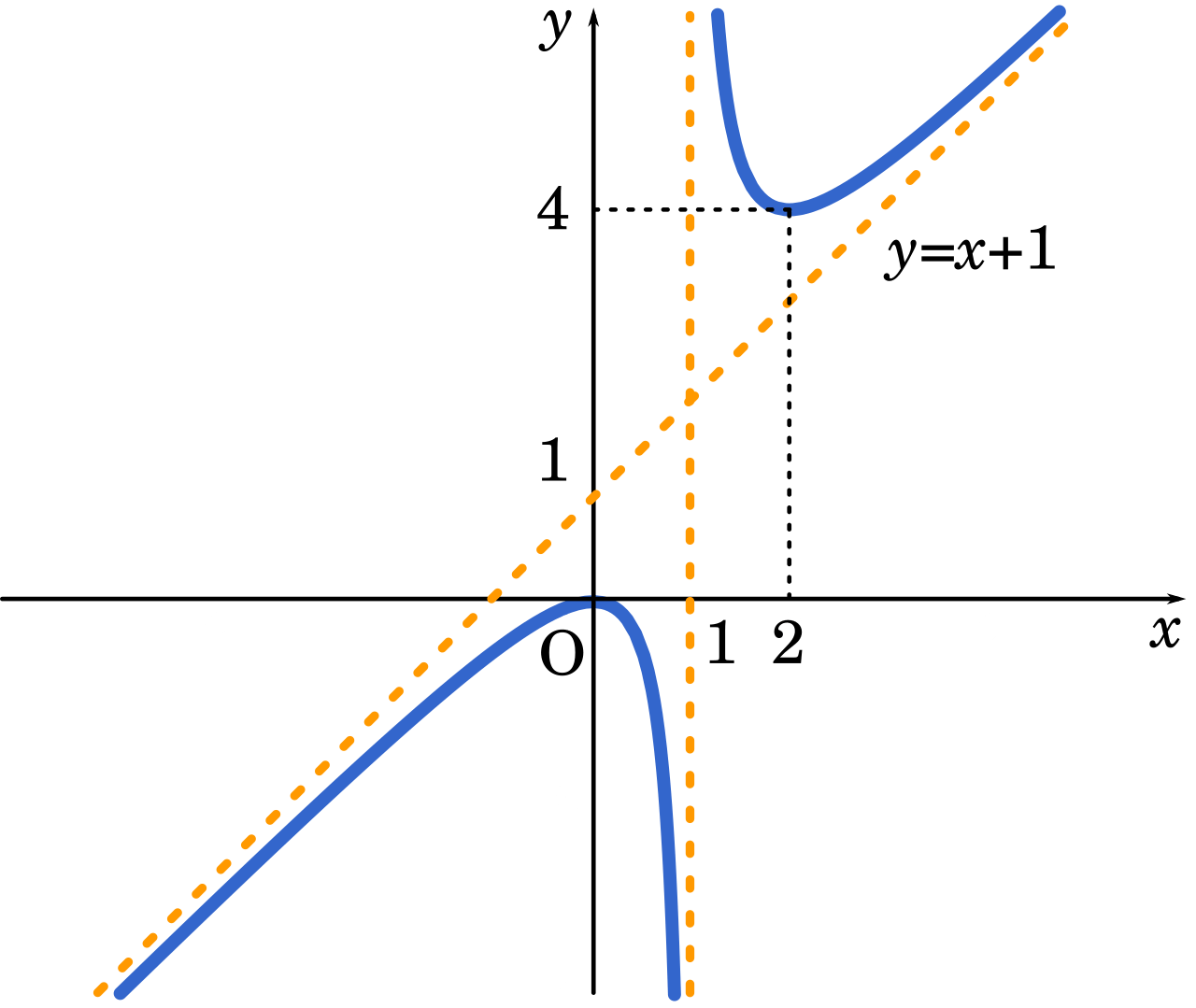


数 微分の応用 ざっくりイメージから漸近線を導く Mm参考書



数学iii 式と曲線 まなびの学園



一次分数関数のグラフと漸近線 高校数学の美しい物語



双曲線とは 式の導出とグラフ 漸近線までイラストでわかりやすく解説
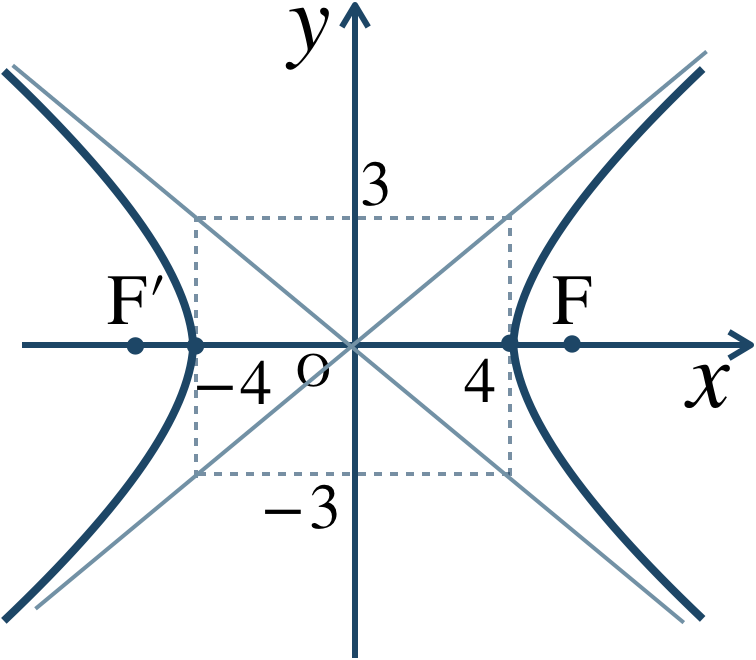


教科書レベルの問題一覧と解答 数学 2次曲線 教科書より詳しい高校数学


分数関数と無理関数のグラフ 漸近線 平行移動と方程式 不等式の解法



数3微分のグラフについてです この問題の漸近線の求め方が分かりません Clear
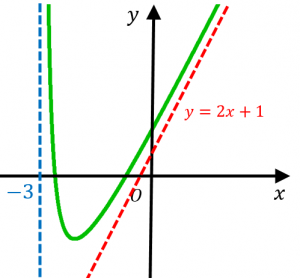


漸近線の求め方3パターン 具体例で学ぶ数学



漸近線の求め方や意味や定義とは 分数関数や双曲線 遊ぶ数学


漸近線 を調べ忘れる君へ漸近線に必要な知識を徹底的にまとめてみました 青春マスマティック



漸近線の求め方を解説しました 無料解説 数学の勉強が一人でできる 医学部受験応援サイト



0 件のコメント:
コメントを投稿